k ist eine natürliche, x jedoch eine reelle Zahl. Da\[{{P}_{n,p}}(k)\approx \varphi_{\mu,\sigma}(x)\] für \(k=x\) gelten muss, muss eine Beziehung zwischen k und x hergestellt werden.

Hierfür werden in diesem Beweis \(\mu\), \(\sigma\) und eine Hilfsvariable z genutzt, so dass gilt:\[k=\mu+z\cdot \sigma=x\]Wegen \(z=\frac{k-\mu}{\sigma}\) sind die z-Werte also k- oder x-Werte, die um \(\mu\) nach links verschoben und um \(\sigma\) gestaucht werden.

Die von der Binomialverteilung eingeschlossene Fläche beträgt 100%. Bei einer Verschiebung der k-Werte um \(\mu\) nach links und einer anschließende Stauchung der Breite der Säulen um \(\sigma\) muss diese natürlich erhalten bleiben!

Eine Verschiebung um \(\mu\) ändert die Fläche nicht. Die Stauchung der Säulenbreite um \(\sigma\) verkleinert die Fläche jedoch, wie man im Bild oben gut erkennen kann (dunkelgrünes Histogramm)! Dies kann man aber ausgleichen, wenn die Länge der Säulen mit \(\sigma\) multipliziert werden. Es ergibt sich folgendes Bild:

Um die ursprüngliche Binomialverteilung mit Hilfe von f(z) beschreiben zu können, muss f(z) nun umgekehrt in der Höhe gestaucht, in der Breite gestreckt und nach rechts verschoben werden:

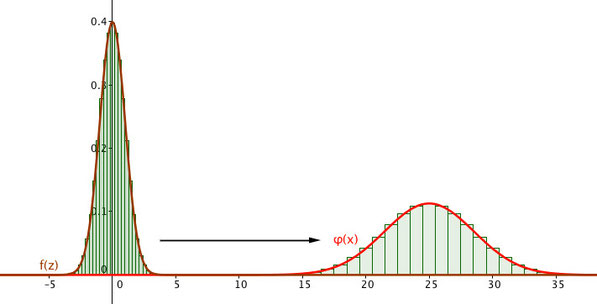
Im Folgenden geht es also darum einen Funktionsterm für f(z) zu finden...